メネラウスの定理(めねらうすのていり、英: Menelaus' theorem)とは、幾何学の定理の1つである。アレクサンドリアのメネラウスにちなんで名付けられた。
定理
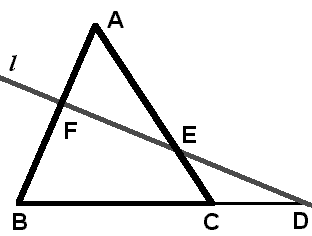
任意の直線lと三角形ABCにおいて、直線lとBC、CA、ABの交点をそれぞれD、E、Fとする。この時、次の等式が成立する。

なお、直線lは、三角形と共有点を持っても持たなくても良い。AからBに行くときにFを通り、BからCに行くときにDを通り、CからAに行くときにEを通る。つまり、A、ABとlの交点、B、BCとlの交点、C、CAとlの交点という順番でたどり、通る辺を順番に分数にすればよい。
証明の方針
証明法はさまざまあるが、ここでは代表的な方針を述べる。
証明1
ABに平行にCから伸ばした線とDEFとの交点をKとする。相似から

が成り立つ。左式のCKを右式に代入、もしくは逆に右式を左式に代入し、整理すれば定理が導かれる。
証明2
ΔABCの各頂点から直線lに垂線をおろす。すると、3組の相似な直角三角形が現れるので、その相似比を考えればよい。
証明3
直線ADと直線BEの交点をGとすると

△AED≠0より

逆
メネラウスの定理は逆も成り立つ。すなわち、任意の三角形ABCに対して、直線AB、BC、CA上に点F、D、Eをとり、D、E、Fのうち三角形ABCの辺上にある点が0個あるいは2個の時、

が成り立つならば、3点D、E、Fは、1直線上にある。
関連項目
外部リンク
- 日本大百科全書(ニッポニカ)『メネラウスの定理』 - コトバンク
- 『メネラウスの定理の覚え方と拡張』 - 高校数学の美しい物語
- メネラウスの定理の覚え方 - YouTube
- Weisstein, Eric W. "Menelaus' Theorem". mathworld.wolfram.com (英語).











