ホンフリー多項式

ホンフリー多項式（ホンフリーたこうしき、HOMFLY polynomial）またはホムフリー多項式とは、位相幾何学の一分野である結び目理論において、有向絡み目に対する2変数の多項式不変量である。

ホンフリー（HOMFLY）とはこの多項式を見出した6人の数学者（J.Hoste , A.Ocneanu , K.Millett, P.Freyd , W.B.R.Lickorish , D.Yetter）の頭文字を並べたもの（頭字語）である。さらに2人の数学者（J. Przytycki , P. Traczyk）の頭文字をつけてフリプモス多項式（FLYPMOTH polynomial）と呼んだり、同様の概念に到達したが論文にして発表しようとしなかっただれか（unknown）を含めてリンプトーフ多項式（LYMPHTOFU polynomial）ということもある[1]。

定義

有向絡み目の射影図 L に対するホンフリー多項式 PL (m , l) を、次の2つのルールによって帰納的に定義する。

  • ルール1
P ◯ ( m , l ) = 1 {\displaystyle P_{\bigcirc }(m,l)=1\,}
ここで○は自明な結び目の任意の射影図である。交点が1つも無い射影図に限らず、自明な結び目の全ての射影図に対して1と定めている点がブラケット多項式のルール1とは異なる。
  • ルール2
3つの射影図 L−, L0, L+ について、射影図の絡み目の成分上の1点の近傍が下図のように異なっており、それ以外の部分は一致しているとする。
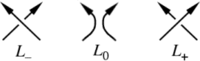
このとき、
l P L + ( m , l ) + l − 1 P L − ( m , l ) + m P L 0 ( m , l ) = 0 {\displaystyle lP_{L_{+}}(m,l)+l^{-1}P_{L_{-}}(m,l)+mP_{L_{0}}(m,l)=0\,}

このような2つのルールを定めておけば、どんな有向絡み目についてもホンフリー多項式を計算することができる。また、そのためのコンピュータ・プログラムも開発されている。

性質

ホンフリー多項式は、有向絡み目に対する多変量となる。つまり、同じ有向絡み目に対するどんな射影図についてホンフリー多項式を計算しても同じ結果になる。また、ホンフリー多項式は成分の全ての向きを逆にしても不変のため、向きのついていない結び目の不変量ともいえる（これはホンフリー多項式が結び目の可逆性を調べる役には立たないということでもある）。

ある絡み目に対するホンフリー多項式中の l {\displaystyle l} を l − 1 {\displaystyle l^{-1}} に置き換えると、元の絡み目の鏡像になる。よって両手型絡み目[注 1]のホンフリー多項式は l について回文的になっている（ただし逆は成り立たない）。

ホンフリー多項式は、スケイン関係式を使って定義されるスケイン多項式の中では最も一般化されたものであり、ジョーンズ多項式とアレクサンダー多項式の両方の情報を含んでいる。実際、ホンフリー多項式において l = i t − 1 , m = i ( t − 1 2 − t 1 2 ) {\displaystyle l=it^{-1},m=i(t^{-{\frac {1}{2}}}-t^{\frac {1}{2}})} を代入するとジョーンズ多項式になり、 l = i , m = i ( t 1 2 − t − 1 2 ) {\displaystyle l=i,m=i(t^{\frac {1}{2}}-t^{-{\frac {1}{2}}})} を代入するとアレクサンダー多項式になる（i は虚数単位）。

絡み目L1 と L2の分離和（L1 ∪ L2）・連結和（L1 # L2）については以下のような公式がある。

P ( L 1 ∪ L 2 ) = − ( l + l − 1 ) m − 1 P ( L 1 ) P ( L 2 ) {\displaystyle P(L_{1}\cup L_{2})=-(l+l^{-1})m^{-1}P(L_{1})P(L_{2})\,}
P ( L 1 # L 2 ) = P ( L 1 ) P ( L 2 ) {\displaystyle P(L_{1}\#L_{2})=P(L_{1})P(L_{2})\,}

後者の連結和について、絡み目のどの成分を連結させるかによって連結後の絡み目はかわるが、その成分の選び方にかかわらずこの式が成立する。つまり、同じホンフリー多項式を持つ異なる絡み目が存在することになり、ホンフリー多項式が完全な不変量ではないことが分かる。結び目に限ったとしても、ホンフリー多項式を持つ異なる有向結び目が無限に存在することが1986年に証明されている[2]。

別の表現

ホンフリー多項式は以下のようなスケイン関係式を使って x , t の多項式として表されることもある[3]。

x P L + ( x , t ) − t P L − ( x , t ) = P L 0 ( x , t ) {\displaystyle xP_{L_{+}}(x,t)-tP_{L_{-}}(x,t)=P_{L_{0}}(x,t)\,}

脚注

  1. ^ ある結び目とその結び目の鏡像が同値のとき、その結び目を両手型結び目という。例えば8の字結び目は両手型結び目であるが、三葉結び目はそうではない。

参考文献

  • C・C・アダムス著、金信泰造訳 『結び目の数学』 培風館、1998年、166-175頁。ISBN 978-4563002541。
  • 村杉邦男 『結び目理論とその応用』 日本評論社、1993年、189-191頁。ISBN 978-4535781993。
  1. ^ 河内明夫 『「結び目理論」　講義7』（大阪市立大学インターネット講座）
  2. ^ T. Kanenobu, Infinitely many knots with the same polynomial invariant, Proc. Amer. Math. Soc. 97(1) (1986), 158–162
  3. ^ V. V. Prasolov, A. B. Sossinsky, Knots, Links, Braids and 3-Manifolds, Amer Mathematical Society, 1993 , p. 36. ISBN 978-0821808986.

外部リンク

  • Weisstein, Eric W. "HOMFLYPolynomial". mathworld.wolfram.com (英語).